哒哒哒哒哒......
想要学好莫比乌斯反演,那么整除分块,你一定要会!
- 首先,可以用到整除分块的形式:
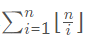
- 这个式子的时间复杂度是O(n)。但是有的时候因为多组数据的要求,可能O(n)并不是正确的时间复杂度。
- 那么这个时候,我们就有一种O(√¯n)的做法。这就是:整除分块!
- 对于每一个
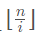 我们可以通过打表的方式
我们可以通过打表的方式(或理性的证明)发现:有许多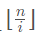 的值是一样的,而且它们呈一个块状分布;
的值是一样的,而且它们呈一个块状分布; - 再通过打表之类的各种方法,我们惊喜的发现对于每一个值相同的块,它的最后一个数就是n/(n/i)。
- 得出这个结论后,我们就可以做O(√¯n)的处理了。
核心代码实现:
for(int l=1,r;l<=n;l=r+1) { r=n/(n/l); ans+=(r-l+1)*(n/l); } 挞哒!
如果你很懒很懒,以至于不想自己模拟的话,那么我们就来举个栗子吧!
当n=22时
首先,手动打表得到(向下取整后的结果):

我们不难看出:

有重复+有分块!
因为是向下取整,所以得到的结果乘以这个块里最大的那个数(i)所得的积在这个块里离原数(n=22)最近;又因为i是从小到大的。
所以:在同一块内,它的最后一个数(序号)就是n/(n/i)。
从代码角度看:
(如果图片看不太清,请将图片用浏览器打开,又大又清晰)
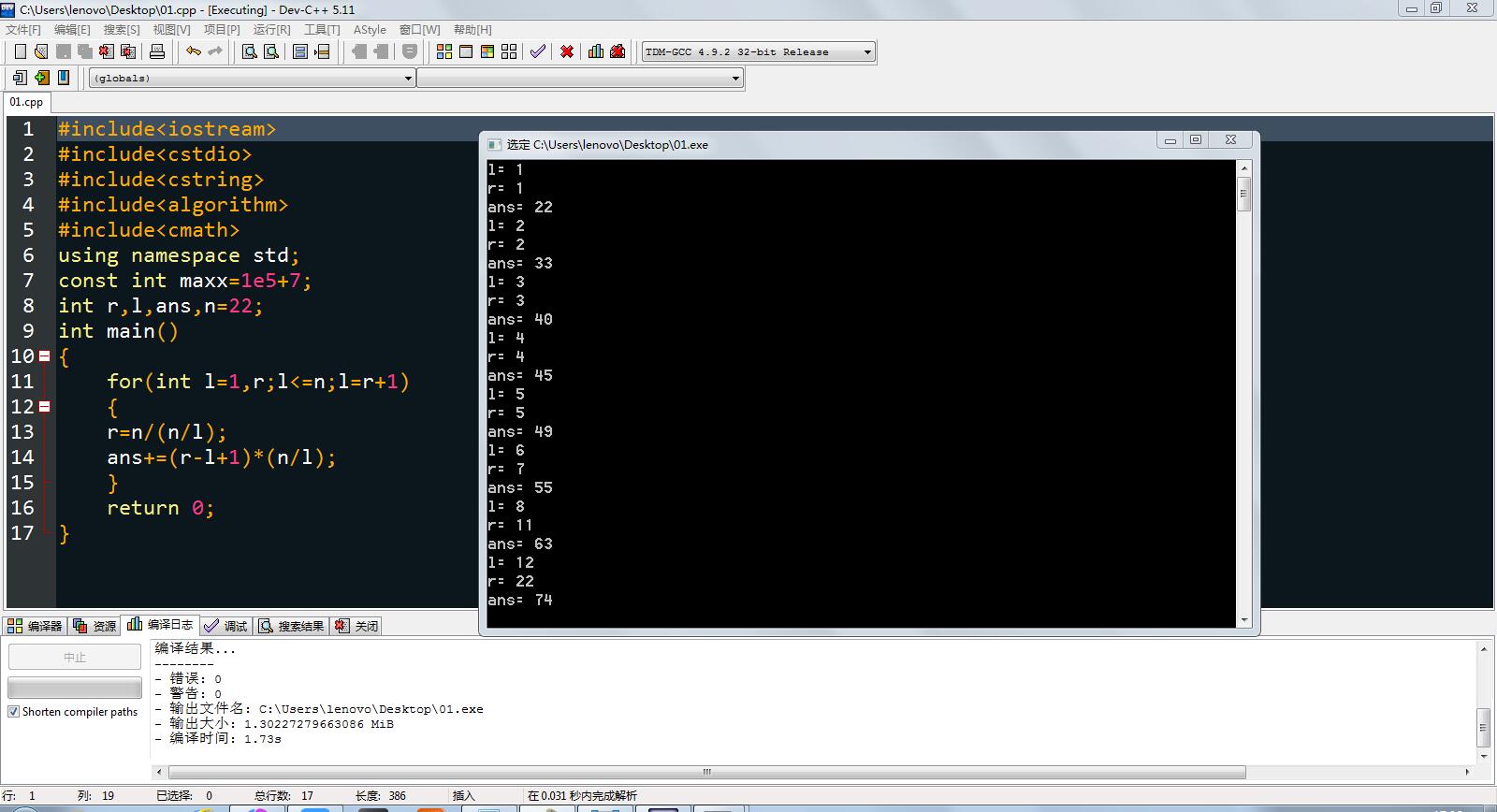
↓
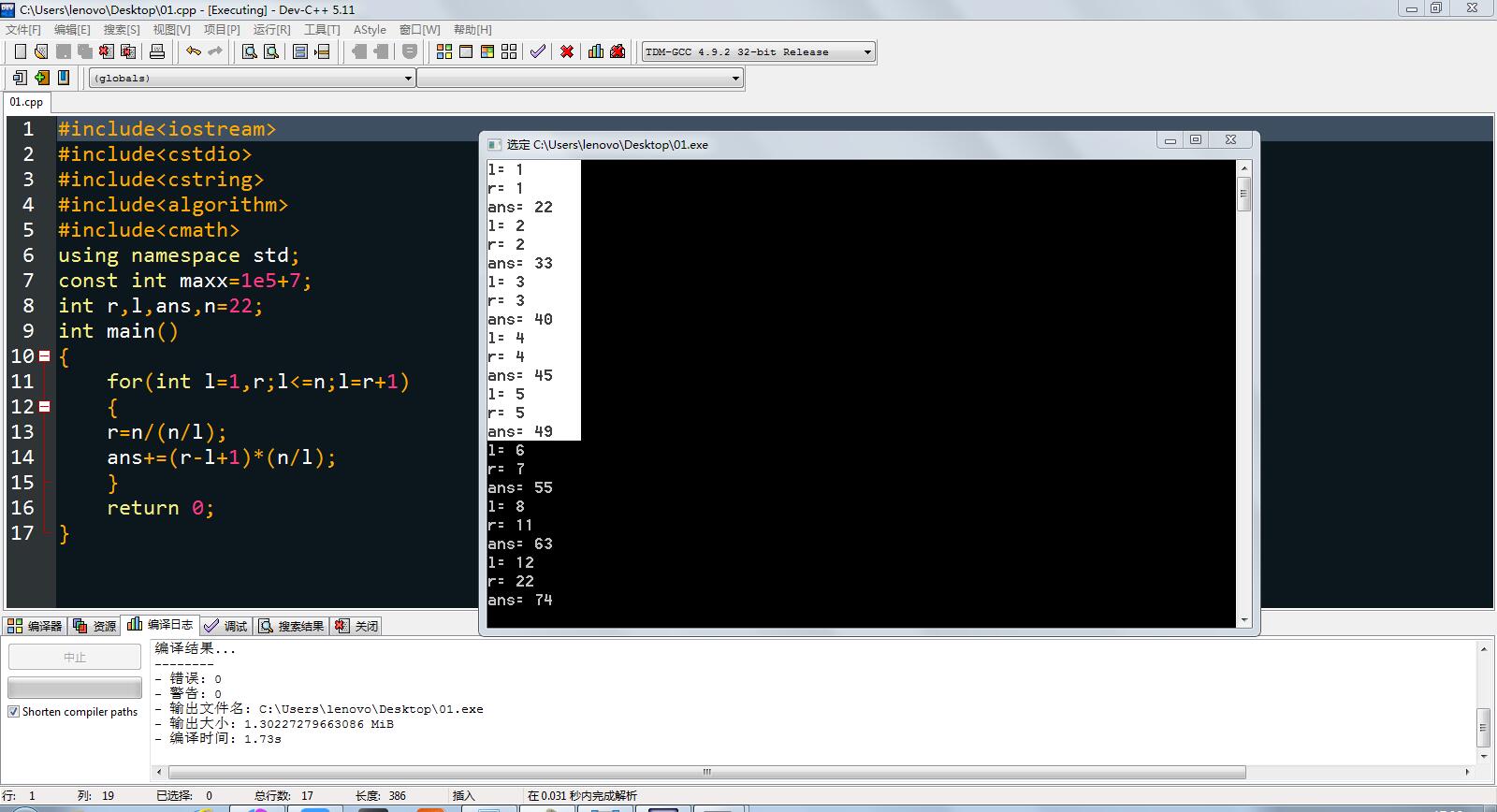
白色部分可以清晰看出,在那个块里只有一个数。
而未标记部分所属的块里有很多数,其实在这里也可以看出整除分块的优越性。
over!
参考相关博客: